Advertisements
Advertisements
प्रश्न
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
उत्तर
Let C be the angle of elevation of sun is θ.
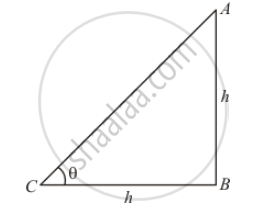
Given that: Height of pole is h meters and length of shadow is h meters. Because length of shadow is equal to the height of pole.
Here we have to find angle of elevation of sun.
So we use trigonometric ratios.
In a triangle ABC,
`⇒ tan θ=(AB)/(BC)`
`⇒ tan θ = h/h`
`⇒ tan θ=1`
`⇒θ=45°`
Hence the angle of elevation of sun is `45°`
APPEARS IN
संबंधित प्रश्न
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
The horizontal distance between two poles is 15 m. The angle of depression of the top of first pole as seen from the top of second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. Use`[sqrt3=1.732]`
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
In figure given ABCD is a rectangle, the value of CE is ____________.

An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
An observer 2.25 m tall is 42.75 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. What is the height of the chimney?
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 meters towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower ____________.
