Question

A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string.

\[\left( \sqrt{3} = 1 . 73 \right)\]

Answer 1

Let AB be the height of kite above the ground and C be the position of the string attached to the kite which is tied at the ground.

Suppose the length of the string be x m.

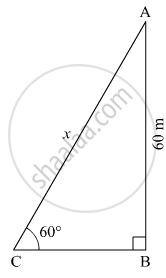
Here, AB = 60 m and ∠ACB = 60º
In right ∆ABC,
\[\sin60^\circ = \frac{AB}{AC}\]
\[ \Rightarrow \frac{\sqrt{3}}{2} = \frac{60}{x}\]
\[ \Rightarrow x = \frac{120}{\sqrt{3}} = 40\sqrt{3}\]
\[ \Rightarrow x = 40 \times 1 . 73 = 69 . 2 m\]

Thus, the length of the string is 69.2 m.