Advertisements
Advertisements
प्रश्न
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string.
उत्तर
Let AB be the height of kite above the ground and C be the position of the string attached to the kite which is tied at the ground.
Suppose the length of the string be x m.
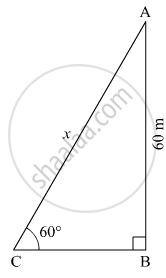
Here, AB = 60 m and ∠ACB = 60º
In right ∆ABC,
\[\sin60^\circ = \frac{AB}{AC}\]
\[ \Rightarrow \frac{\sqrt{3}}{2} = \frac{60}{x}\]
\[ \Rightarrow x = \frac{120}{\sqrt{3}} = 40\sqrt{3}\]
\[ \Rightarrow x = 40 \times 1 . 73 = 69 . 2 m\]
Thus, the length of the string is 69.2 m.
APPEARS IN
संबंधित प्रश्न
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
An observed from the top of a 150 m tall lighthouse, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
As observed form the top of a lighthouse, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° and 60° . Determine the distance travelled by the ship during the period of observation.
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
If the ratio of the height of a tower and the length of its shadow is `sqrt3:1`, what is the angle of elevation of the Sun?
From the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be 38° and 60° respectively. Find the height of the lamp post (tan 38° = 0.7813, `sqrt(3)` = 1.732)
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats. `(sqrt(3) = 1.732)`
If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
If a man standing on a platform 3 meters above the surface of a lake observes a cloud and its reflection in the lake, then calculate the angle of elevation of the cloud.
Two poles of heights 25 m and 35 m stand vertically on the ground. The tops of two poles are connected by a wire, which is inclined to the horizontal at an angle of 30°. Find the length of the wire and the distance between the poles.
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
