Advertisements
Advertisements
Question
Prove that a parallelogram circumscribing a circle is a rhombus.
Solution
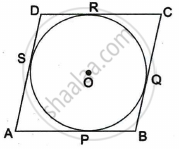
Let ABCD be the rhombus circumscribing the circle with centre O, such that AB, BC, CD and DA touch the circle at points P, Q, R and S respectively. We know that the tangents drawn to a circle from an exterior point are equal in length.
∴ AP = AS ...(i) [tangents from A]
BP = BQ ...(ii) [tangents from B]
CR = CQ ...(iii) [tangents from C]
DR = DS ...(iv) [tangents from D]
∴ AB + CD = AP + BP + CR + DR
= AS + BQ + CQ + DS ...[From (i), (ii), (iii), (iv)]
= (AS + DS) + (BQ + CQ)
= AD + BC
Hence, (AB + CD) = (AD + BC)
⇒ 2AB = 2AD
[∵ opposite sides of a parallelogram are equal]
⇒ AB = AD
∴ CD = AB = AD = BC
Hence, ABCD is a rhombus.
APPEARS IN
RELATED QUESTIONS
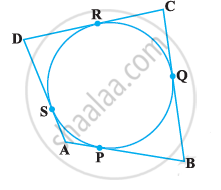
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
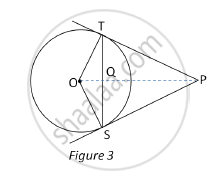
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°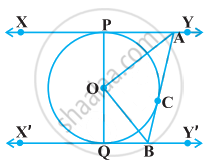
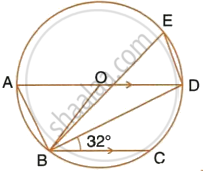
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
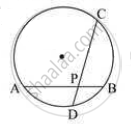
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
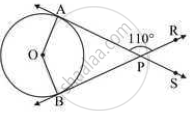
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
A tangent is drawn from a point at a distance of 17 cm of circle C(0, r) of radius 8 cm. The length of its tangent is ______
The number of tangents drawn at a point of the circle is/are ______
The length of the tangent from an external point P on a circle with centre O is ______
The length of the tangent from an external point on a circle is ______
In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

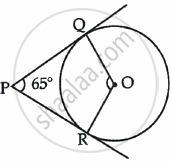
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.