Advertisements
Advertisements
प्रश्न
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4(AN2 + CM2) =
पर्याय
4 AC2
5 AC2
- \[\frac{5}{4} {AC}^2\]
6 AC2
उत्तर
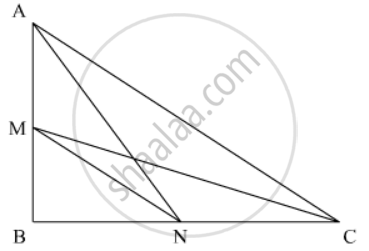
M is the mid-point of AB.
∴ \[BM = \frac{AB}{2}\]
N is the mid-point of BC.
∴\[BN = \frac{BC}{2}\]
Now,
`AN^2+CM^2=(AB^2+(BC)^2)+((AB)^2+BC^2)`
`=AB^2+BC^2+1/4AB^2+BC^2`
`=5/4(AB^2+BC^2)`
`⇒ 4(AN^2+CM^2)=5AC^2`
Hence option (b) is correct.
APPEARS IN
संबंधित प्रश्न
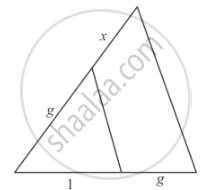
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
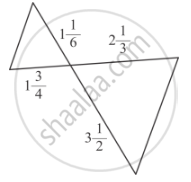
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
In ∆ABC, D and E are points on side AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 3.3 cm, then AC =
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
