Advertisements
Advertisements
प्रश्न
In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
उत्तर
Given PM = 15 cm,MQ = 10 cm , NR = 8 cm and PN = 12 cm .
\[\frac{PN}{PR} = \frac{12cm}{20cm} = \frac{3}{5} \left( PN = PR - NR = 20 - 8 = 12cm \right)\]
\[ \therefore \frac{PM}{PQ} = \frac{PN}{PR}\]
So, by the converse of basic proportionality theorem MN || QR.
APPEARS IN
संबंधित प्रश्न
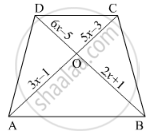
In the below figure, If AB || CD, find the value of x.
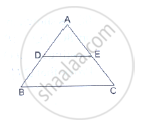
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 7.2cm, AE = 6.4cm, AB = 12cm and AC = 10cm.
In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
State SSS similarity criterion.
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
