Advertisements
Advertisements
प्रश्न
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
पर्याय
12 cm
8 cm
- \[8\sqrt{2} cm\]
- \[12\sqrt{2} cm\]
उत्तर
Given: One side of isosceles right triangle is 4√2cm
To find: Length of the hypotenuse.
We know that in isosceles triangle two sides are equal.

In isosceles right triangle ABC, let AB and AC be the two equal sides of measure 4√2cm.
Applying Pythagoras theorem, we get
`BC^2=AB^2+AC^2`
`BC^2=(4sqrt2)^2+(4sqrt2)^2`
`BC^2=32+32`
`BC^2=64`
`BC=8`
Hence correct answer is `b`.
APPEARS IN
संबंधित प्रश्न
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
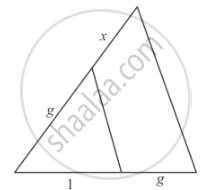
In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC2 = 2 AC. CD
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
In an equilateral triangle ABC if AD ⊥ BC, then
