Advertisements
Advertisements
प्रश्न
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
उत्तर
GIVEN: ΔABC and ΔDEF are similar triangles such that AB = 3cm, BC = 2cm, CA = 2.5cm and EF = 4cm.
TO FIND: Perimeter of ΔDEF.
We know that if two triangles are similar then their corresponding sides are proportional.
Hence, `(AB)/(DE)=(BC)/(EF)=(CA)/(FD)`
Substituting the values, we get
`(AB)/(BC)=(DE)/(EF)`
`3/2=(DE)/4`
`DE=6 cm`........(1)
Similarly,
`(CA)/(BC)=(DF)/(EF)`
`2.5/2=(DF)/(4)`
`DF= 5cm`...........(2)
P[erimeter of `Δ DEF = DE +EF+DF`
`=6+4+5`
`= 15 cm`
APPEARS IN
संबंधित प्रश्न
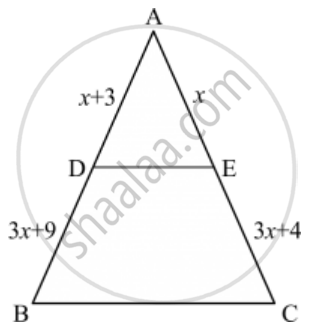
In the below figure, If AB || CD, find the value of x.
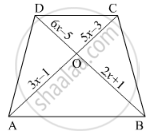
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
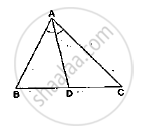
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR?
If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
In the given figure, the value of x for which DE || AB is