Advertisements
Advertisements
प्रश्न
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR?
उत्तर
Given: ΔABC and ΔPQR are similar triangles. Area of ΔABC: Area of ΔPQR = 9:16 and BC = 4.5cm.
To find: Length of QR
We know that the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.
Hence,
`(ar(Δ ABC))/(ar(ΔPQR))=(BC^2)/(QR^2)`
`9/16=4.5^2/(QR^2)`
`9/12=4.5^2/(QR^2)`
`QR^2= (4.5^2xx16)/(9)`
`QR^2=36`
`QR= 6 cm`
APPEARS IN
संबंधित प्रश्न
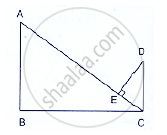
In Figure below, if AB ⊥ BC, DC ⊥ BC and DE ⊥ AC, Prove that Δ CED ~ ABC.
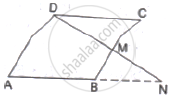
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
ABCD is a trapezium such that BC || AD and AD = 4 cm. If the diagonals AC and BD intersect at O such that \[\frac{AO}{OC} = \frac{DO}{OB} = \frac{1}{2}\], then BC =
∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
