Advertisements
Advertisements
प्रश्न
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR?
उत्तर
Given: ΔABC and ΔPQR are similar triangles. Area of ΔABC: Area of ΔPQR = 9:16 and BC = 4.5cm.
To find: Length of QR
We know that the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.
Hence,
`(ar(Δ ABC))/(ar(ΔPQR))=(BC^2)/(QR^2)`
`9/16=4.5^2/(QR^2)`
`9/12=4.5^2/(QR^2)`
`QR^2= (4.5^2xx16)/(9)`
`QR^2=36`
`QR= 6 cm`
APPEARS IN
संबंधित प्रश्न
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
In the given figure, DE || BD. Determine AC and AE.

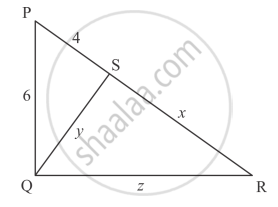
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
In ∆ABC, D and E are points on side AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 3.3 cm, then AC =
If ∆ABC is an equilateral triangle such that AD ⊥ BC, then AD2 =
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
