Advertisements
Advertisements
प्रश्न
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
विकल्प
2 cm
4 cm
6 cm
8 cm
उत्तर
Given: XY is drawn parallel to the base BC of a ΔABC cutting AB at X and AC at Y. AB = 4BX and YC = 2 cm.
To find: AY
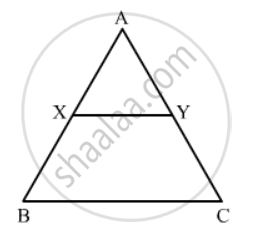
In ΔAXY and ΔABC,
\[\angle AXY = \angle B \left( \text{Corresponding angles} \right)\]
\[\angle A = \angle A \left( \text{Common} \right)\]
\[ \therefore ∆ AXY~ ∆ ABC \left( \text{AA similarity} \right)\]
We know that if two triangles are similar, then their sides are proportional.
It is given that AB = 4BX.
Let AB = 4x and BX = x.
Then, AX = 3x
`(AX)/(BX)=(AY)/(YC)`
`(3x)/(1x)=(AY)/2`
`AY=(3x xx2)/(1x)`
`AY= 6cm`
Hence the correct answer is `C`
APPEARS IN
संबंधित प्रश्न
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
