Advertisements
Advertisements
Question
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
Options
12 m
14 m
13 m
11 m
Solution
Given: Two poles of heights 6m and 11m stand vertically upright on a plane ground. Distance between their foot is 12 m.
To find: Distance between their tops.
Let CD be the pole with height 6m.
AB is the pole with height 11m, distance between their foot i.e. DB is 12 m.
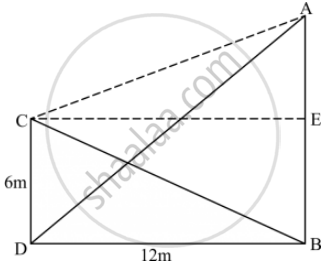
Let us assume a point E on the pole AB which is 6m from the base of AB.
Hence
AE = AB − 6 = 11 − 6 = 5 m
Now in right triangle AEC, Applying Pythagoras theorem
AC2 = AE2 + EC2
AC2 = 52 + 122 (since CDEB forms a rectangle and opposite sides of rectangle are equal)
AC2 = 25 + 144
AC2 = 169
`AC= 13cm`
Thus, the distance between their tops is 13m.
Hence correct answer is `C`.
APPEARS IN
RELATED QUESTIONS
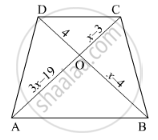
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
