Advertisements
Advertisements
Question
The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
Solution
Since the ratio of areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.
`\text{(Area of triangle)}/\text{(Area of larger triangle)}=\text{(Corresponding side of smaller triangle)}^2/\text{(Corresponding side of larger triangle)}^2`
`36/100=3^2/\text{(Corresponding side of larger triangle)}^2`
`\text{(Corresponding side of larger triangle)}^2= (9xx100)/(36)`
`\text{(Corresponding side of larger triangle)}^2 100/4`
`\text{(Corresponding side of larger triangle)}^2=25`
`\text{(Corresponding side of larger triangle)}^2= 5`
Hence, the length of the corresponding side of the larger triangle is `5 cm`
APPEARS IN
RELATED QUESTIONS
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
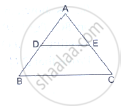
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the road. Assuming that her string (from the tip of her road to the fly) is taut, how much string does she have out (in the given figure)? If she pulls the string at the rate of 5 cm per second, what will the horizontal distance of the fly from her after 12 seconds.

In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
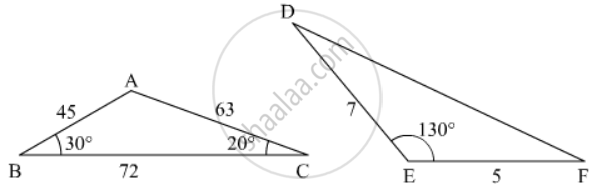
In the given figure the measure of ∠D and ∠F are respectively
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
