Advertisements
Advertisements
प्रश्न
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
उत्तर
In triangle ABC, P and Q are points on sides AB and AC respectively such that `PQ|| BC`.
In ΔAPQ and ΔABC,
Substituting value AP = 3cm,AB=10cm and PQ = 3cm, we get
`(AP)/(AB)=(3)/(BC)`
By cross multiplication we get
`4 xx BC = 3xx10`
`BC = (3xx10)/4`
`BC = 30/4`
`BC = 7.5 cm`
Hence, the value of BC is 7.5 cm.
APPEARS IN
संबंधित प्रश्न
In below figure, If AB || CD, find the value of x.
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
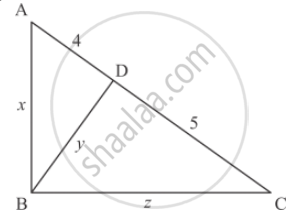
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
State basic proportionality theorem and its converse.
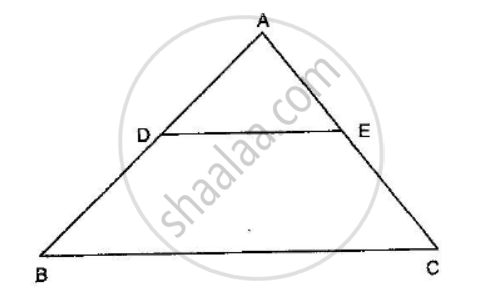
In the given figure, DE || BC and \[AD = \frac{1}{2}BD\]. If BC = 4.5 cm, find DE.
The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
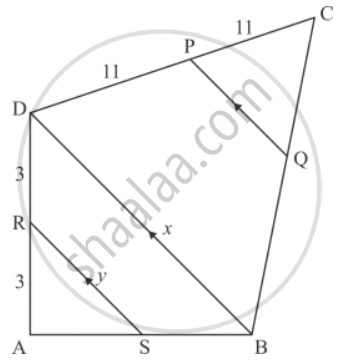
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.