Advertisements
Advertisements
Question
In a quadrilateral ABCD, ∠B = 90°. If AD2 = AB2 + BC2 + CD2 then prove that ∠ACD = 90°.
Solution

In quadrilateral ABCD, we have
∠B = 90°
So, `AC^2=AB^2+BC^2` (Pythagoras theorem)
and
`AD^2=AB^2+BC^2+CD^2` (Given)
So,
`AD^2=AB62+BC^2+CD^2`
`AD^2=AC^2+CD^2`
Hence, ∠ACD = 90° (Converse of Pythagoras theorem)
APPEARS IN
RELATED QUESTIONS
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
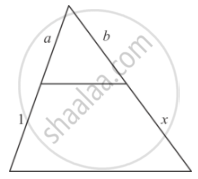
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
