Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, ∠B = 90°. If AD2 = AB2 + BC2 + CD2 then prove that ∠ACD = 90°.
उत्तर

In quadrilateral ABCD, we have
∠B = 90°
So, `AC^2=AB^2+BC^2` (Pythagoras theorem)
and
`AD^2=AB^2+BC^2+CD^2` (Given)
So,
`AD^2=AB62+BC^2+CD^2`
`AD^2=AC^2+CD^2`
Hence, ∠ACD = 90° (Converse of Pythagoras theorem)
APPEARS IN
संबंधित प्रश्न
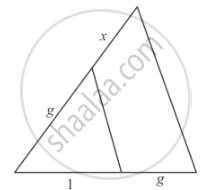
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
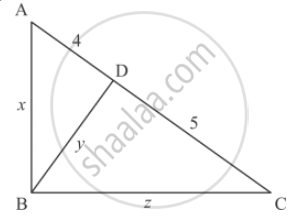
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR?
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
