Question

∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is

पर्याय

• 2 : 1

• 1 : 2

• 4 : 1

• 1 : 4

Answer 1

Given: ΔABC and ΔBDE are two equilateral triangles such that D is the midpoint of BC.

To find: Ratio of areas of ΔABC and ΔBDE.

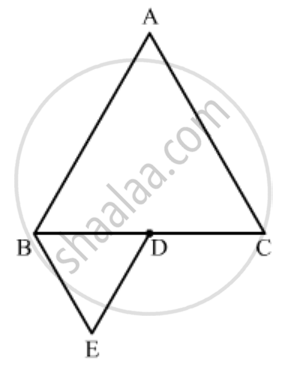
ΔABC and ΔBDE are equilateral triangles; hence they are similar triangles.

Since D is the midpoint of BC, BD = DC.

We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

`\text{ar(Δ ABC)}/\text{ar(Δ BDE)}=((BC)/(BD))^2`

`\text{ar(Δ ABC)}/\text{ar(Δ BDE)}=((BD+DC)/(BD))^2`[D is the midpoint of BC]

`\text{ar(Δ ABC)}/\text{ar(Δ BDE)}=((BD+DC)/(BD))^2`

`\text{ar(Δ ABC)}/\text{ar(Δ BDE)}=((2BD)/(BD))^2`

`\text{ar(Δ ABC)}/\text{ar(Δ BDE)}=4/1`

Hence the correct answer is `C`