Advertisements
Advertisements
प्रश्न
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
पर्याय
16 cm
12 cm
8 cm
4 cm
उत्तर
Given: ΔABC and ΔDEF are similar triangles such that 2AB = DE and BC = 8 cm.
To find: EF
We know that if two triangles are similar then there sides are proportional.
Hence, for similar triangles ΔABC and ΔDEF
`(AB)/(DE)=(BC)/(EF)=(CA)/(FD)`
`(AB)/(DE)=(BC)/(EF)`
`1/2=8/(EF)`
`EF= 16cm`
Hence the correct answer is `a`.
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
In the given figure, DE || BD. Determine AC and AE.

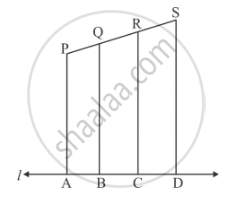
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
In the given figure, Δ AHK ∼ Δ ABC. If AK = 8 cm, BC = 3.2 cm and HK = 6.4 cm, then find the length of AC.

