Advertisements
Advertisements
प्रश्न
In the given figure, Δ AHK ∼ Δ ABC. If AK = 8 cm, BC = 3.2 cm and HK = 6.4 cm, then find the length of AC.

उत्तर
ΔAHK ∼ ΔABC (The triangles are similar, which means corresponding sides are proportional.)
AK = 8 cm
BC = 3.2 cm
HK = 6.4 cm
We need to find the length of the AC.
Using the proportionality of the corresponding sides of similar triangles, we have:
`(AC)/(AK)` = `(BC)/(HK)`
Substituting the given lengths:
`(AC)/8` = `3.2/6.4`
This simplifies to:
`(AC)/8 = 1/2`
Therefore:
AC = `8×1/2`
AC = 4 cm
Thus, the length of AC in the triangle is 4 cm.
APPEARS IN
संबंधित प्रश्न
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
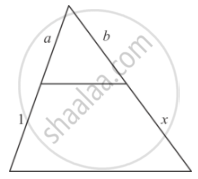
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
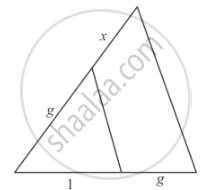
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
In a quadrilateral ABCD, ∠B = 90°. If AD2 = AB2 + BC2 + CD2 then prove that ∠ACD = 90°.
If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
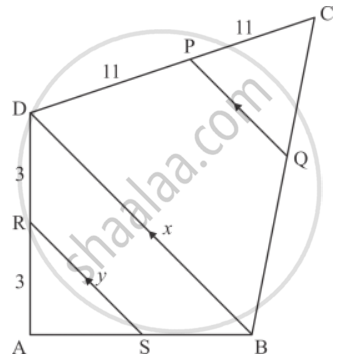
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
