Advertisements
Advertisements
प्रश्न
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
उत्तर
We are given ABCD is a trapezium with AB||DC
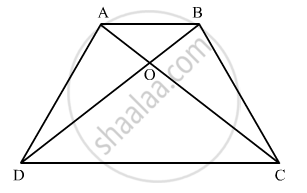
Consider the triangles AOB and COD in which
`∠ AOB = ∠COD `
`∠ ABO = ∠ODC ` (ALTERNATIVE ANGLE)
`∠ BAO = ∠DCA ` (ALTERNATIVE ANGLE)
Therefore, ` ∆ODC ∼ ∆ OBA`
`⇒ (AO)/(OC)=(BO)/(DO)=(AB)/(CD)`
`⇒ (AO)/(OC)=(BO)/(DO) `
Hence we have proved that O, the point of intersection of diagonals, divides the two diagonals in the same ratio.
We are given AB = 3CD and we have to prove that `(ar∆ OCD)/(ar∆ OAB)=1/9`
We already have proved that AOB and COD are similar triangles
So
`(ar∆ OCD)/(ar∆ OAB)= (CD^2)/(AB^2)`
`(ar∆ OCD)/(ar∆ OAB)= (CD^2)/(3CD^2)`
`(ar∆ OCD)/(ar∆ OAB)= 1/9`
Hence, Prove that `(ar∆ OCD)/(ar∆ OAB)= 1/9`
APPEARS IN
संबंधित प्रश्न
the below given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ΔABC is 54 cm2, then find the lengths of sides AB and AC.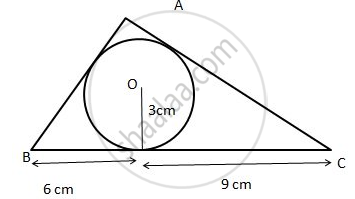
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
In ∆ABC, D and E are points on side AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 3.3 cm, then AC =
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
∆ABC ∼ ∆DEF, ar(∆ABC) = 9 cm2, ar(∆DEF) = 16 cm2. If BC = 2.1 cm, then the measure of EF is
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
