Advertisements
Advertisements
प्रश्न
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
उत्तर

The circumference of the circular park = 352 m.
Let r be the radius of the circular park.
Then, 2πr = 352
`2 xx 22/7 xx r` = 352
r = `(352 xx 7)/(2 xx 22)` = 56 m
Area of circular park = πr2
= `22/7 xx (56)^2`
= `22/7 xx 56 xx 56`
= 22 × 8 × 56
= 9856 m2
Now, the circular park's radius with road,
R = 56 + 7 = 63 m
∴ Circular park area with a road
= πR2
= `22/7 xx (63)^2`
= `22/7 xx 63 xx 63`
= 22 × 9 × 63
= 12474 m2
So, Area of road = Area of circular park with road – Area of circular park
= 12474 – 9856
= 2618 m2
Hence, the area of road is 2618 m2.
APPEARS IN
संबंधित प्रश्न
Prove that the tangents at the extremities of any chord make equal angles with the chord.
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
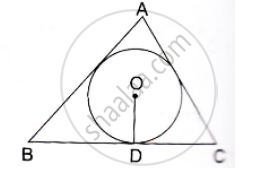
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
In the given figure, if ∠ABC = 45°, then ∠AOC =
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

In the given figure, the area enclosed between the two concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
Twice the radius is ________________
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
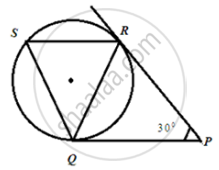
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
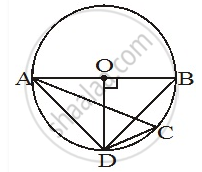
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD.
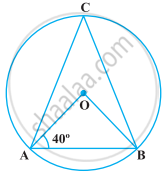
In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
