Advertisements
Advertisements
प्रश्न
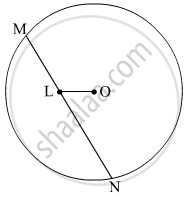
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
उत्तर
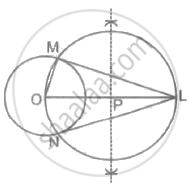
Steps of construction:
- Draw a circle with an O in the centre and a radius of 3 cm.
- Line the outside of the circle with a point so that OL = 7 cm.
- Make a perpendicular bisector of OL segment. It crosses OL at P.
- Draw another circle overlapping the given circle at points M and N, with Pas as the centre and radius equal to PL.
- Join with LM and LN.
Tangents to the circle are segments LM and LN.
Justification: If we join O and M, then
∠OML = 90° ......[Angle in a semi-circle]
So, LM ⊥ OM
The radius of the circle is shown by OM in the figure.
Therefore, from point L, LM is a tangent to the circle.
Similarly, from point L, LN is a tangent to the circle.
APPEARS IN
संबंधित प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
In Fig., if AB = AC, prove that BE = EC
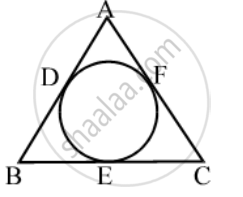
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
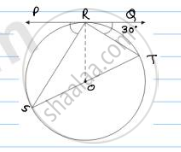
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
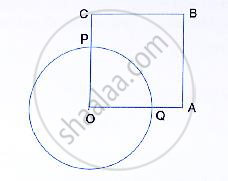
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
Two concentric circles with center O have A, B, C, D as the points of intersection with the lines L shown in the figure. If AD = 12 cm and BC s = 8 cm, find the lengths of AB, CD, AC and BD.
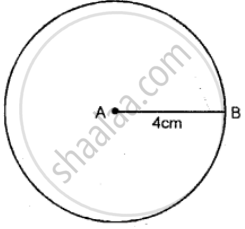
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
Find the radius of the circle
Diameter = 24 cm
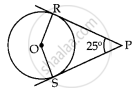
In the given figure, if ZRPS = 25°, the value of ZROS is ______
If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
From the figure, identify a segment.

A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
