Advertisements
Advertisements
Question
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
Solution
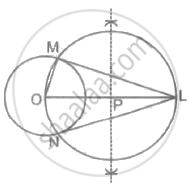
Steps of construction:
- Draw a circle with an O in the centre and a radius of 3 cm.
- Line the outside of the circle with a point so that OL = 7 cm.
- Make a perpendicular bisector of OL segment. It crosses OL at P.
- Draw another circle overlapping the given circle at points M and N, with Pas as the centre and radius equal to PL.
- Join with LM and LN.
Tangents to the circle are segments LM and LN.
Justification: If we join O and M, then
∠OML = 90° ......[Angle in a semi-circle]
So, LM ⊥ OM
The radius of the circle is shown by OM in the figure.
Therefore, from point L, LM is a tangent to the circle.
Similarly, from point L, LN is a tangent to the circle.
APPEARS IN
RELATED QUESTIONS
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
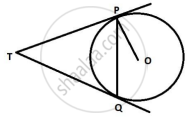
PA and PB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
Write True or False. Give reason for your answer.
Sector is the region between the chord and its corresponding arc.
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
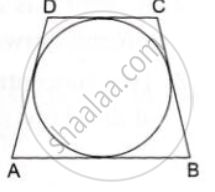
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
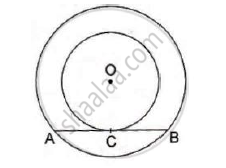
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

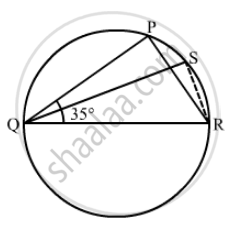
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
If O is the centre of the circle, find the value of x in each of the following figures

The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
Draw circle with the radii given below.
4 cm
Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
A part of circumference of a circle is called as _______
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.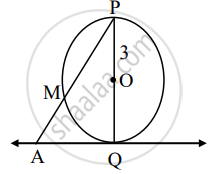
Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
