Advertisements
Advertisements
प्रश्न
In Fig., if AB = AC, prove that BE = EC
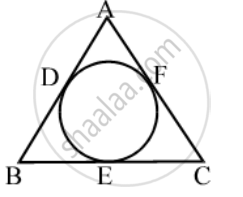
उत्तर
Since tangents from an exterior point to a circle are equal in length.
∴ AD = AF [Tangents from A]
BD = BE [Tangents from B]
CE = CF [Tangents from C]
Now,
AB = AC
⇒ AB – AD = AC – AD [Subtracting AD from both sides]
⇒ AB – AD = AC – AF [Using (i)]
⇒ BD = CF ⇒ BE = CF [Using (ii)]
⇒ BE = CE [Using (iii)]
APPEARS IN
संबंधित प्रश्न
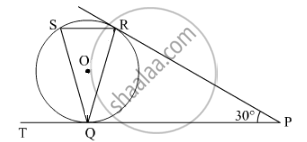
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure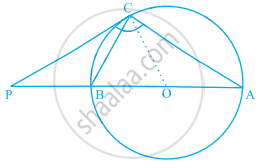
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

