Advertisements
Advertisements
प्रश्न
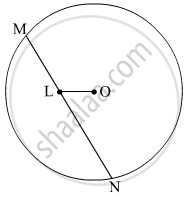
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
उत्तर
seg MN is a chord of a circle with centre O.
Draw OP ⊥ MN and join OM.

MP = PN = `(MN)/2 = 25/2`units (Perpendicular drawn from the centre of a circle on its chord bisects the chord)
∴ LP = MP − ML = `25/2-9=7/2`units
In right ∆OPL,
\[{OL}^2 = {LP}^2 + {OP}^2 \]
\[ \Rightarrow OP = \sqrt{{OL}^2 - {LP}^2}\]
\[ \Rightarrow OP = \sqrt{5^2 - \left( \frac{7}{2} \right)^2}\]
\[ \Rightarrow OP = \sqrt{25 - \frac{49}{4}}\]
\[ \Rightarrow OP = \sqrt{\frac{51}{4}} = \frac{1}{2}\sqrt{51} \] units
In right ∆OPM,
\[{OM}^2 = {MP}^2 + {OP}^2 \]
\[ \Rightarrow OM = \sqrt{\left( \frac{25}{2} \right)^2 + \left( \frac{\sqrt{51}}{2} \right)^2}\]
\[ \Rightarrow OM = \sqrt{\frac{625 + 51}{4}}\]
\[ \Rightarrow OM = \sqrt{\frac{676}{4}}\]
\[ \Rightarrow OM = \sqrt{169} = 13 \] units
Thus, the radius of the circle is 13 units.
APPEARS IN
संबंधित प्रश्न
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA.
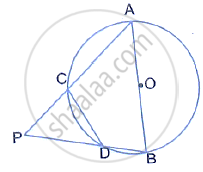
Is AC produced and BD produced meet at point P; show that ∠APB = 60°
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
The circumference of a circle is 22 cm. The area of its quadrant (in cm2) is
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
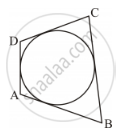
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.


In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
A part of circumference of a circle is called as _______
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

