Advertisements
Advertisements
प्रश्न
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

उत्तर
Given: ∠POR = 130°
So, ∠TSR = \[\frac{1}{2}\angle POR = \frac{1}{2} \times 130^o = 65^o = \angle2\] (Since angle subtended by the arc at the centre is double the angle subtended by it at the remaining part of the circle)
∠POQ = 180º − ∠POR = 180º − 130º = 50º .....(2) (Linear pair)
In
Δ POQ, \[\angle1 + \angle POQ + \angle OQP = 180^o\]
\[ \Rightarrow \angle1 + 50^o + 90^o = 180^o\]
\[ \Rightarrow \angle1 = 40^o\]
\[\angle1 + \angle POQ + \angle OQP = 180^o\]
\[ \Rightarrow \angle1 + 50^o + 90^o = 180^o\]
\[ \Rightarrow \angle1 = 40^o\]
\[Now \angle1 + \angle2 = 40^o + 65^o = 105^o\]
APPEARS IN
संबंधित प्रश्न
In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
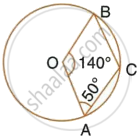
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.
In the given figure, PQ is chord of a circle with centre O an PT is a tangent. If
∠QPT = 60°, find the ∠PRQ.

In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

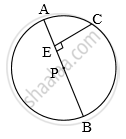
In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
Find the radius of the circle
Diameter = 76 cm
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
