Advertisements
Advertisements
प्रश्न
In the given figure, PQ is chord of a circle with centre O an PT is a tangent. If
∠QPT = 60°, find the ∠PRQ.

उत्तर
We know that the radius and tangent are perpendicular at their point of contact
∴ ∠OPT = 90°
Now,∠OPQ = ∠OPT - ∠QPT = 90° - 60° = 30°
Since, OP = OQas born is radius
∴ ∠OPQ = ∠OQP = 30° (Angles opposite to equal sides are equal)
Now, In isosceles, POQ
∠POQ + ∠OPQ +∠OQP = 180° (Angle sum property of a triangle)
⇒ ∠POQ =180° - 30° - 30° =120°
Now, ∠POQ + reflex ∠POQ = 360° (Complete angle)
⇒ reflex ∠POQ = 360° - 120° = 240°
We know that the angle subtended by an arc at the centre double the angle subtended by the arc at any point on the remaining part of the circle
∴ ∠PRQ `=1/2 `( reflex ∠POQ)= 120°
APPEARS IN
संबंधित प्रश्न
In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.
Write True or False. Give reason for your answer.
Line segment joining the centre to any point on the circle is a radius of the circle.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

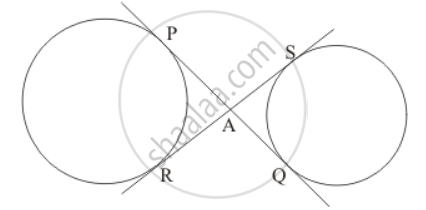
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
AD is a diameter of a circle and AB is a chord If AD = 30 cm and AB = 24 cm then the distance of AB from the centre of the circle is
Find the diameter of the circle
Radius = 10 cm
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.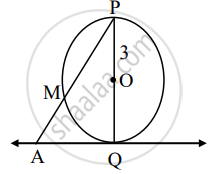
A line through the point of contact and passing through centre of the circle is known as ______
