Advertisements
Advertisements
प्रश्न
Write True or False. Give reason for your answer.
Line segment joining the centre to any point on the circle is a radius of the circle.
विकल्प
True
False
उत्तर
True.
All the points on the circle are at equal distances from the centre of the circle, and this equal distance is called as radius of the circle.
APPEARS IN
संबंधित प्रश्न
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
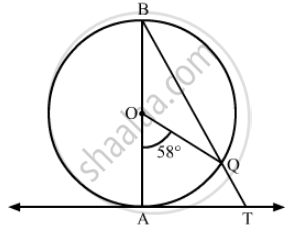
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
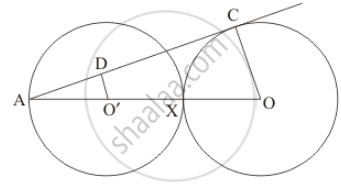
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
Can the length of a chord of a circle be greater than its diameter ? Explain.
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
