Advertisements
Advertisements
प्रश्न
Write True or False. Give reason for your answer.
Line segment joining the centre to any point on the circle is a radius of the circle.
पर्याय
True
False
उत्तर
True.
All the points on the circle are at equal distances from the centre of the circle, and this equal distance is called as radius of the circle.
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
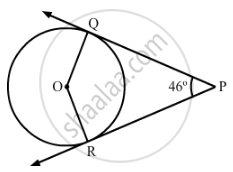
(A) 67°
(B) 134°
(C) 44°
(D) 46°
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Prove that the tangents at the extremities of any chord make equal angles with the chord.
Write True or False. Give reason for your answer.
A circle is a plane figure.
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
