Advertisements
Advertisements
प्रश्न
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
उत्तर
et XBY and PCQ be two parallel tangents to a circle with centre O.
Construction: Join OB and OC.
Draw OA∥XY
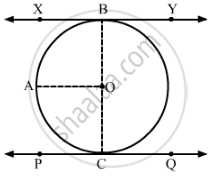
Now, XB∥AO
⇒ ∠XBO + ∠AOB = 180° (sum of adjacent interior angles is 180°)
Now, ∠XBO = 90° (A tangent to a circle is perpendicular to the radius through the point of contact)
⇒ 90° + ∠AOB = 180°
⇒ ∠AOB = 180° − 90° = 90°
Similarly, ∠AOC = 90°
∴ ∠AOB + ∠AOC = 90° + 90° = 180°
Hence, BOC is a straight line passing through O.
Thus, the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
APPEARS IN
संबंधित प्रश्न
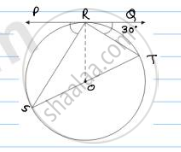
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

Number of circles that can be drawn through three non-collinear points is
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

The ratio between the circumference and diameter of any circle is _______
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
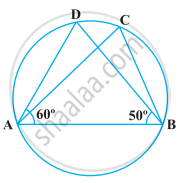
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
