Advertisements
Advertisements
प्रश्न
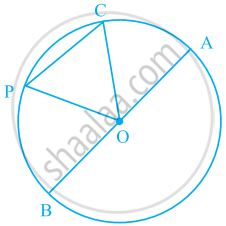
Number of circles that can be drawn through three non-collinear points is
पर्याय
1
0
2
3
उत्तर
Suppose we are given three non-collinear points as A, B and C

1. Join A and B.
2. Join B and C.
3. Draw perpendicular bisector of AB and BC which meet at O as centre of the circle.
So basically we can only draw one circle passing through three non-collinear points A, B and C.
APPEARS IN
संबंधित प्रश्न
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

Use the figure given below to fill in the blank:
______ is a chord of the circle.

Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
A circle of radius 3 cm can be drawn through two points A, B such that AB = 6 cm.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.