Advertisements
Advertisements
प्रश्न
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
पर्याय
45°
60°
75°
90°
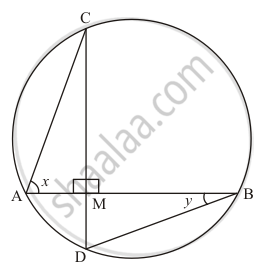
उत्तर
90°
We are given the following figure
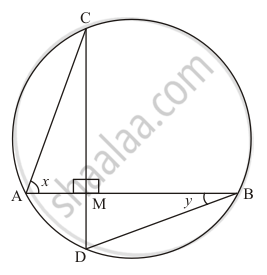
∠ACD = ∠ABD (Angle in the same segment are equal)
⇒ ∠ACD = y
Consider the ΔACM in which
`angleACM + x + 90° = 180°`
` y + x + 90° = 180°`
`x + y = 90°`
APPEARS IN
संबंधित प्रश्न
In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
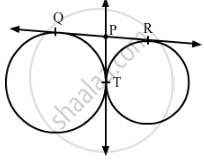
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
Prove that two different circles cannot intersect each other at more than two points.
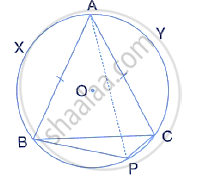
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

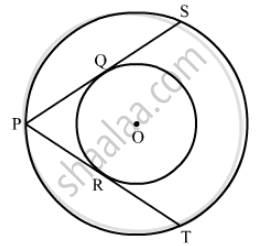
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

