Advertisements
Advertisements
प्रश्न
Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
उत्तर
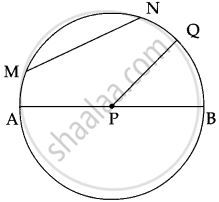
In a circle, P is the centre.
AB is a diameter.
PQ is a radius
MN is a chord
संबंधित प्रश्न
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
In fig., O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
Draw a circle of radius 6 cm. In the circle, draw a chord AB = 6 cm.
(i) If O is the center of the circle, join OA and OB.
(ii) Assign a special name to ∆AOB
(iii) Write the measure of angle AOB.
Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
