Advertisements
Advertisements
प्रश्न
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

उत्तर

Given:
OA = 6 cm
OB = 4 cm
AP = 8 cm
Consider ∆OAP.
By Pythagoras' theorem, we have
OA2 + AP2 = PO2
⇒ 62 + 82 = PO2
⇒ PO2 = 100
⇒ PO = 10 cm
Now, consider ∆OBP.
By Pythagoras' theorem, we have
OB2 + BP2 = PO2
⇒ 42 + BP2 = 102
⇒ BP2 = 84
⇒ BP =
Hence, the length of BP is
APPEARS IN
संबंधित प्रश्न
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.
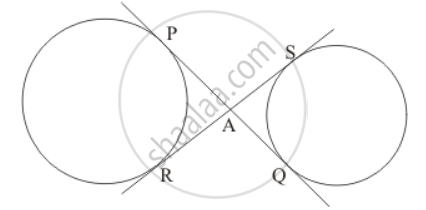
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
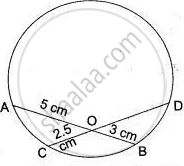
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
