Advertisements
Advertisements
Question
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

Solution

Given:
OA = 6 cm
OB = 4 cm
AP = 8 cm
Consider ∆OAP.
By Pythagoras' theorem, we have
OA2 + AP2 = PO2
⇒ 62 + 82 = PO2
⇒ PO2 = 100
⇒ PO = 10 cm
Now, consider ∆OBP.
By Pythagoras' theorem, we have
OB2 + BP2 = PO2
⇒ 42 + BP2 = 102
⇒ BP2 = 84
⇒ BP =
Hence, the length of BP is
APPEARS IN
RELATED QUESTIONS
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
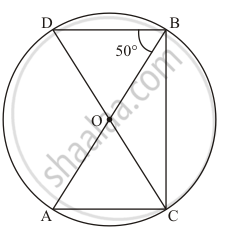
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
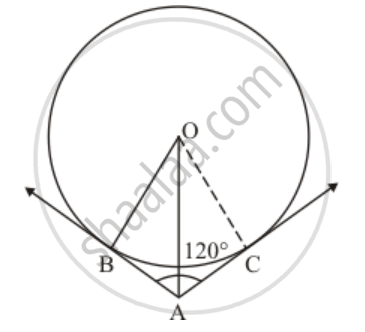
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
Draw circle with the radii given below.
2 cm
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
In the given figure, O is the centre of the circle. Name a chord, which is not the diameter of the circle.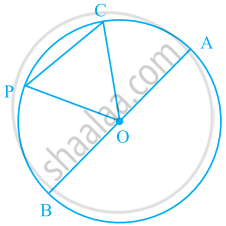
From the figure, identify the centre of the circle.