Advertisements
Advertisements
Question
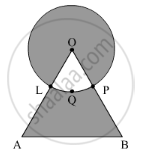
Find the area of shaded region in Fig. 4, where a circle of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm. (Use π = 3.14 and\[\sqrt{3}\] =1.73)
Solution
Given:
Radius of the circle (r) = 6 cm
Side of the equilateral triangle (a) = 12 cm
Now,
Area of the shaded region = Area of the circle with centre O + Area of the equilateral triangle OAB − 2(Area of the sector OLP)
\[= \pi r^2 + \frac{\sqrt{3}}{4} a^2 - 2\frac{\theta}{360^o}\pi r^2 \]
\[ = \pi \left( 6 \right)^2 + \frac{\sqrt{3}}{4} \left( 12 \right)^2 - 2\frac{60^o}{360^o}\pi \left( 6 \right)^2 (\text{Because OAB is an equilateral triangle})\]
\[ = 36\pi + \frac{\sqrt{3}}{4}\left( 144 \right) - 2\frac{60^o}{360^o}\pi\left( 36 \right)\]
APPEARS IN
RELATED QUESTIONS
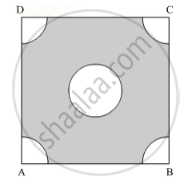
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and `sqrt3 `= 1.73205]

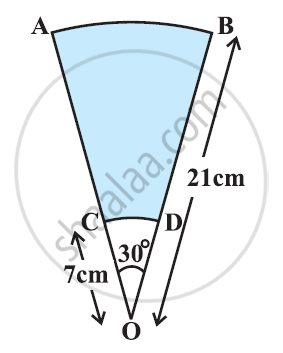
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
The perimeter of a triangular field is 240m, and its sides are in the ratio 25:17:12. Find the area of the field. Also, find the cost of ploughing the field at ₹ 40 per `m^2`
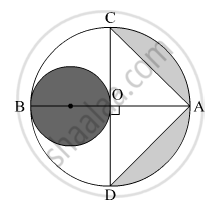
In Fig.5, AB and CD are two diameters of a circle with centre O, which are perpendicular to each other. OB is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. `[\text{Use}pi=22/7]`
In Figure 4, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. (Use π = 3.14)
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time, it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
Find the area of the shaded region in figure.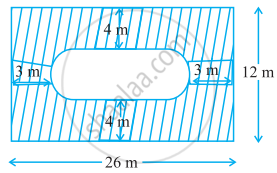
Read the following passage:
|
For the inauguration of 'Earth day' week in a school, badges were given to volunteers. Organisers purchased these badges from an NGO, who made these badges in the form of a circle inscribed in a square of side 8 cm.
|
Based on the above information, answer the following questions:
- What is the area of square ABCD?
- What is the length of diagonal AC of square ABCD?
- Find the area of sector OPRQO.
OR
Find the area of remaining part of square ABCD when area of circle is excluded.


