Advertisements
Advertisements
Question
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
Solution
Given: An equilateral triangle ABC in which D, E, and F are the midpoints of sides BC, CA and AB respectively.
To prove: The centroid and circumference are coincident.
Construction: Draw medians AD, BE and CF.
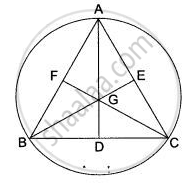
Proof:
Let G be the centroid of ΔABC i.e., the point of intersection of AD, BE, and CF. In triangles BEC and BFC, we have
∠ B = ∠ C = 60°
BC = BC
and BF = CE ...[ ∵ AB = AC ⇒ `1/2"AB" = 1/2` AC ⇒ BF = CE ]
∴ ΔBEC = ΔBFC
⇒ BE = CF ...(i)
Similarly,
Δ CAF and Δ CAD
⇒ CF = AD ...(ii)
From (i) and (ii),
AD = BE = CF
⇒ `2/3"AD" = 2/3 BE = 2/3"CF"`
CG = `2/3"CF"`
GA = `2/3"AD"`
GB = `2/3 "BE"`
GA = GB = GC
⇒ G is the equidistant from the vertices
⇒ G is the circumcentre of ΔABC.
Hence, the centroid and circumcentre are coincident.
APPEARS IN
RELATED QUESTIONS
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
Fill in the blank:
A point whose distance from the centre of a circle is greater than its radius lies in ..................... of the circle.
true or false
A circle is a plane figure.
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

A line segment joining any point on the circle to its center is called the _____________ of the circle
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
From the figure, identify the centre of the circle.
From the figure, identify a diameter.