Advertisements
Advertisements
Question
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
Solution
Draw a quadrilateral ABCD inscribed in a circle having centre O.
Given, ∠ADC = 130°
Since, ABCD is a quadrilateral inscribed in a circle, therefore ABCD becomes a cyclic quadrilateral.
∵ Since, the sum of opposite angles of a cyclic quadrilateral is 180°.
∴ ∠ADC + ∠ABC = 180°
⇒ 130° + ∠ABC = 180°
⇒ ∠ABC = 50°
Since, AB is a diameter of a circle, then AB subtends an angle to the circle is right angle.
∴ ∠ACB = 90°
In ΔABC, ∠BAC + ∠ACB + ∠ABC = 180° ...[By angle sum property of a triangle]
⇒ ∠BAC + 90° + 50° = 180°
⇒ ∠BAC = 180° – (90° + 50°)
= 180° – 140°
= 40°
APPEARS IN
RELATED QUESTIONS
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
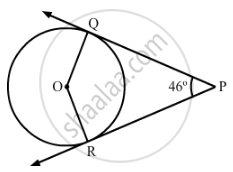
(A) 67°
(B) 134°
(C) 44°
(D) 46°
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
Prove that the tangents at the extremities of any chord make equal angles with the chord.
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
Find the radius of the circle
Diameter = 76 cm
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.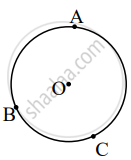
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
