Advertisements
Advertisements
Question
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
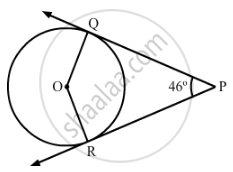
(A) 67°
(B) 134°
(C) 44°
(D) 46°
Solution
Given: ∠QPR = 46°
PQ and PR are tangents.
Therefore, the radius drawn to these tangents will be perpendicular to the tangents.
So, we have OQ ⊥ PQ and OR ⊥ RP.
⇒ ∠OQP = ∠ORP = 90∘
So, in quadrilateral PQOR, we have
∠OQP +∠QPR + ∠PRO + ∠ROQ = 360∘
⇒ 90° + 46° + 90° + ∠ROQ = 360∘
⇒ ∠ROQ = 360∘ − 226∘ = 134∘
Hence, the correct option is B.
APPEARS IN
RELATED QUESTIONS
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
true or false
Sector is the region between the chord and its corresponding arc.
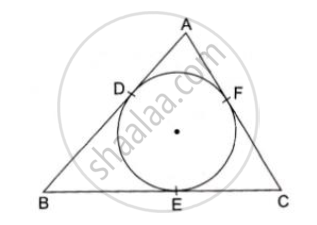
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
Draw circle with the radii given below.
2 cm
A line through the point of contact and passing through centre of the circle is known as ______
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
A circle of radius 3 cm can be drawn through two points A, B such that AB = 6 cm.
