Advertisements
Advertisements
प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
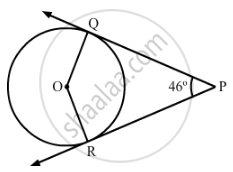
(A) 67°
(B) 134°
(C) 44°
(D) 46°
उत्तर
Given: ∠QPR = 46°
PQ and PR are tangents.
Therefore, the radius drawn to these tangents will be perpendicular to the tangents.
So, we have OQ ⊥ PQ and OR ⊥ RP.
⇒ ∠OQP = ∠ORP = 90∘
So, in quadrilateral PQOR, we have
∠OQP +∠QPR + ∠PRO + ∠ROQ = 360∘
⇒ 90° + 46° + 90° + ∠ROQ = 360∘
⇒ ∠ROQ = 360∘ − 226∘ = 134∘
Hence, the correct option is B.
APPEARS IN
संबंधित प्रश्न
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
Draw a circle of radius 6 cm. In the circle, draw a chord AB = 6 cm.
(i) If O is the center of the circle, join OA and OB.
(ii) Assign a special name to ∆AOB
(iii) Write the measure of angle AOB.
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
From the figure, identify the centre of the circle.
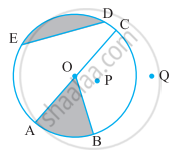
From the figure, identify a sector.

