Advertisements
Advertisements
प्रश्न
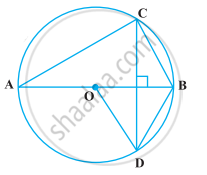
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
उत्तर
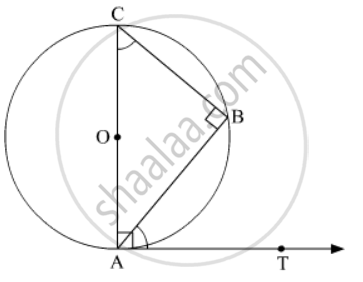
In the given figure,
AC is the diameter.
So,
AT is the tangent at point A.
Thus,
\[ \Rightarrow \angle BCA + 90^o + \angle CAT - \angle BAT = 180^o \]
\[ \Rightarrow \angle BCA + 90^o + 90 - \angle BAT = 180^o \]
\[ \Rightarrow \angle BCA = \angle BAT\]
Hence Proved
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
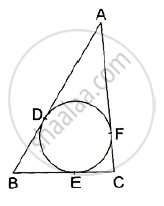
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
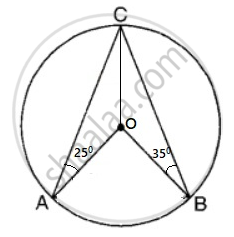
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
A circle of radius 3 cm can be drawn through two points A, B such that AB = 6 cm.
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.