Advertisements
Advertisements
प्रश्न
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
उत्तर
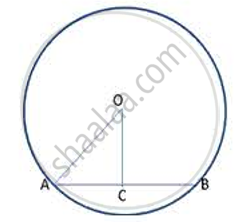
AC = CB ----(1) (Perpendicular from centre to a chord bisects the chord)
In right t. ACO,
By Pythagoras theorem, OA2 = OC2 + AC2
132 -122 = AC2
AC2 = 169 - 144 = 25
AC = 5 cm
∴ length of chord AB = 2AC (from (1))
APPEARS IN
संबंधित प्रश्न
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
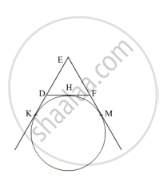
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
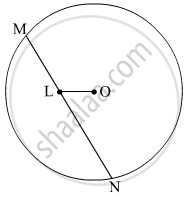
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.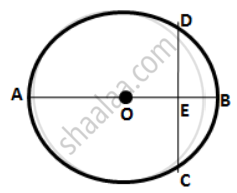
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
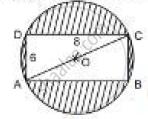
Find the radius of the circle
Diameter = 24 cm
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
The length of tangent from an external point on a circle is always greater than the radius of the circle.
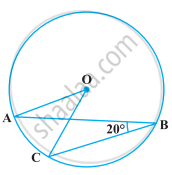
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.