Advertisements
Advertisements
प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
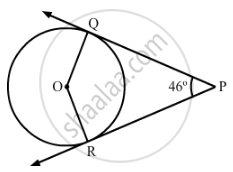
(A) 67°
(B) 134°
(C) 44°
(D) 46°
उत्तर
Given: ∠QPR = 46°
PQ and PR are tangents.
Therefore, the radius drawn to these tangents will be perpendicular to the tangents.
So, we have OQ ⊥ PQ and OR ⊥ RP.
⇒ ∠OQP = ∠ORP = 90∘
So, in quadrilateral PQOR, we have
∠OQP +∠QPR + ∠PRO + ∠ROQ = 360∘
⇒ 90° + 46° + 90° + ∠ROQ = 360∘
⇒ ∠ROQ = 360∘ − 226∘ = 134∘
Hence, the correct option is B.
APPEARS IN
संबंधित प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
Find the diameter of the circle
Radius = 10 cm
Find the radius of the circle
Diameter = 30 cm
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
