Advertisements
Advertisements
Question
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
Solution
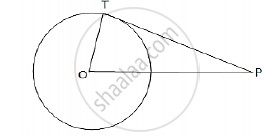
Let O be the center of the given circle.
Let P be a point, such that
OP = 17 cm.
Let OT be the radius, where
OT = 5cm
Join TP, where TP is a tangent.
Now, tangent drawn from an external point is perpendicular to the radius at the point of contact.
∴ OT ⊥ PT
In the right Δ OTP,we have:
`OP^2 = OT^2 +TP^2 ` [By Pythagoras’ theorem:]
`TP = sqrt(OP^2 - OT^2)`
`=sqrt(17^2 -8^2)`
` =sqrt(289-64)`
`= sqrt(225)`
= 15 cm
∴ The length of the tangent is 15 cm.
APPEARS IN
RELATED QUESTIONS
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
In Fig., if AB = AC, prove that BE = EC
Fill in the blanks:
A circle divides the plane, on which it lies, in __________ parts.
Write True or False. Give reason for your answer.
Sector is the region between the chord and its corresponding arc.
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
Number of circles that can be drawn through three non-collinear points is
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
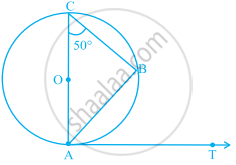
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.