Advertisements
Advertisements
Question
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
Solution
Consider a circle with center O and radius OA = 8cm = r, AB = 15 cm.
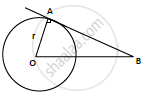
(AB) tangent is drawn at A (point of contact)
At point of contact, we know that radius and tangent are perpendicular.
In ΔOAB, ∠OAB = 90°, By Pythagoras theorem
𝑂𝐵2 = 𝑂𝐴2 + 𝐴𝐵2
`OB = sqrt(8^2 + 15^2)`
`=sqrt(64+225)`
`= sqrt(289)`
= 17 cm
∴ 𝑂𝐵 = 17 𝑐𝑚
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
Draw a circle of radius 4.8 cm and mark its center as P.
(i) Draw radii PA and PB such that ∠APB = 45°.
(ii) Shade the major sector of the circle
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
If the radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is ______
