Advertisements
Advertisements
Question
If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
Solution
Given,
PQ = 24 cm
OQ = 25 cm
OP = radius = ?
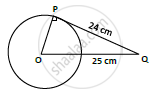
P is point of contact, At point of contact, tangent and radius are perpendicular to each other
∴ ΔPOQ is right angled triangle ∠OPQ = 90°
By Pythagoras theorem,
๐๐2 + ๐๐2 = ๐๐2
⇒ 242 + ๐๐2 = 252
⇒`PO = sqrt((25)^2 − (24)^2) = sqrt(625 − 576)`
= `sqrt(49)` = 7๐๐
∴ ๐๐ = ๐๐๐๐๐ข๐ = 7๐๐
APPEARS IN
RELATED QUESTIONS
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
Fill in the blank
A continuous piece of a circle is ............... of the circle
The greatest chord of a circle is called its
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.
Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.
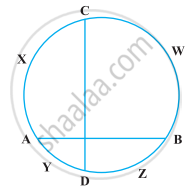
From the figure, identify a point in the exterior.
Say true or false:
Two diameters of a circle will necessarily intersect.
