Advertisements
Advertisements
рдкреНрд░рд╢реНрди
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
рдЙрддреНрддрд░
Consider a circle with center O and radius OA = 8cm = r, AB = 15 cm.
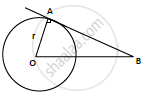
(AB) tangent is drawn at A (point of contact)
At point of contact, we know that radius and tangent are perpendicular.
In ΔOAB, ∠OAB = 90°, By Pythagoras theorem
ЁЭСВЁЭР╡2 = ЁЭСВЁЭР┤2 + ЁЭР┤ЁЭР╡2
`OB = sqrt(8^2 + 15^2)`
`=sqrt(64+225)`
`= sqrt(289)`
= 17 cm
∴ ЁЭСВЁЭР╡ = 17 ЁЭСРЁЭСЪ
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
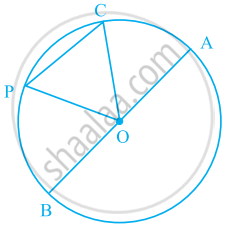
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
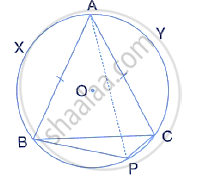
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
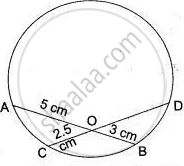
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
Use the figure given below to fill in the blank:
AB is a ______ of the circle.
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.
In the given figure, O is the centre of the circle. Name all radii of the circle.
