Advertisements
Advertisements
Question
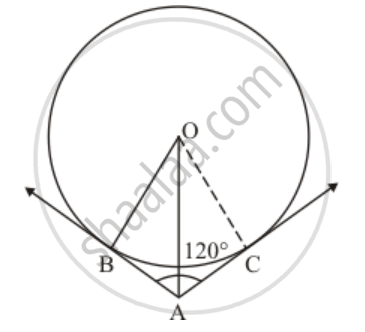
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
Solution
Consider Δ OAB and Δ OAC.
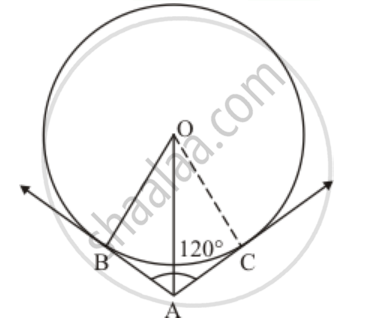
We have,
OB = OC (Since they are radii of the same circle)
AB = AC (Since length of two tangents drawn from an external point will be equal)
OA is the common side.
Therefore by SSS congruency, we can say that Δ OAB and Δ OAC are congruent triangles.
Therefore,
∠OAC = ∠OAC
It is given that,
`∠OAB +∠OAC=120^o`
`2∠OAB=120^o`
`∠OAB=60^o`
We know that,
`cos∠OAB =(AB)/(OA) `
`cos 60^o =(AB)/(OA) `
We know that,
`cos 60^o =1/2`
Therefore,
`1/2=(AB)/(OA)`
OA = 2AB
APPEARS IN
RELATED QUESTIONS
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
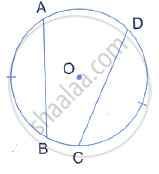
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
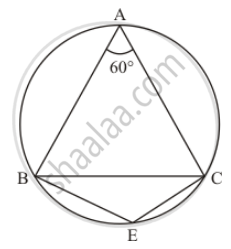
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
Use the figure given below to fill in the blank:
______ is a chord of the circle.

Use the figure given below to fill in the blank:
AB is a ______ of the circle.

Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
