Advertisements
Advertisements
Question
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
Solution
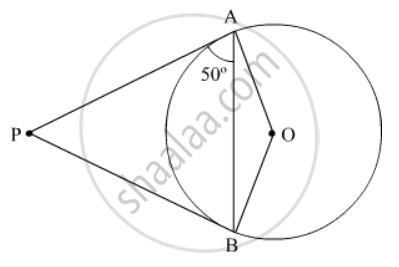
It is given that PA and PB are tangents to the given circle.
OB = OA (Radii of the circle)
APPEARS IN
RELATED QUESTIONS
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

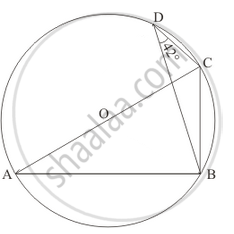
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
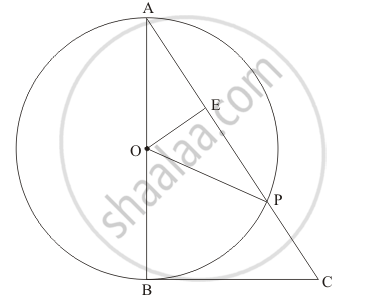
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
