Advertisements
Advertisements
Question
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

Solution
Given, PA and PB are the tangents to a circle with center O and CD is a tangent at E and PA = 14 cm.
Tangents drawn from an external point are equal.
∴ PA = PB, CA = CE and DB = DE
Perimeter of Δ PCD = PC + CD + PD
= (PA- CA)+( CE +DE) +( PB- DB)
= (PA -CE)+ (CE+ DE)+( PB- DE)
=(PA+ PB)
= 2PA(∵ PA= PB)
=(2×14) cm
= 28 cm
=28 cm
∴ Perimeter of ΔPCD = 28cm.
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
A circle divides the plane, on which it lies, in __________ parts.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
C(O, r1) and C(O, r2) are two concentric circles with r1 > r2 AB is a chord of C(O, r1) touching C(O, r2) at C then ______
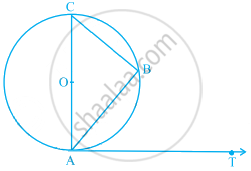
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
